Two years ago, I was tasked to write a program that generates RPM package repositories from a large pool of packages. The pool is a set of directories that contain all packages that were ever built for a given Miracle Linux release, and the program would be used to pick specific packages from the pool and generate repositories for yum and dnf. The existing program had hard-coded rules for package selection that made it require frequent repairs, and it didn’t play nice with modularity packages. Since the new solution should be an improvement over the old one, I decided to separate the rules from the code, and for this I needed a small domain-specific language. I had already written a lot of absurd things in Bash at the time, so naturally I had to see if a parser could be another of those things.
Making up a language
I didn’t know what kind of criteria would be used for the package selection, but I wanted to give the user as much freedom as possible. An RPM package’s properties can be queried using query tags, so I decided that the language must allow easy access to these tags. The following is what I came up with.
BaseOS : name == "kernel" &&
version == "5.6.10" &&
release >= "1.el9" &&
release <= "2.el9" &&
arch == "amd64";
BaseOS : name =~ "^miraclelinux-";
AppStream : modularitylabel.module == "nginx" &&
modularitylabel.stream == "1.14" &&
buildtime < 1690001217;
The left-hand side of a rule (that is, the part on the left of the colon) is the
name of the destination repository while the right-hand side is a logical expression
that defines criteria for the packages to be added. The property names used on the
right-hand side are the query tags for rpm --queryformat, so this language allows
the user to filter RPM packages in all kinds of ways. In the case of the
modularitylabel tag, it goes one step further: the information behind this tag has
four components that one doesn’t usually compare all at once, so I wanted to allow
users to query the individual components of this tag.
The first rule in the example tells the program to search for all packages with name
kernel and version 5.6.10 and a release that is between 1.el9 and 2.el9
(inclusive) that were built for the amd64 architecture. The newest package that
meets these criteria will be added to the BaseOS repository.
The =~ operator used in the second rule means regular expression match. This rule
selects all packages whose name starts with miraclelinux-. Since this will match
multiple packages (miraclelinux-release, miraclelinux-logos, etc), this will cause
the newest version of each of the matched packages to be added to the BaseOS repository.
The rule does not specify the architecture either, so a package will be added multiple
times if it is available for multiple architectures.
The last rule selects all packages from the modularity stream nginx:1.14 that were
built before 13:46:57 on July 22, 2023, Japanese Standard Time.
Grammar of the language
The first step in any compiler or interpreter is the lexer (or tokenizer), which turns an input into a stream of tokens. Tokens are similar to words in natural languages, in that they can be used to form statements. When we study a foreign language, we try to understand which words are the subject, object, verb, etc of a sentence. That’s essentially what a parser does.
To write a correct lexer for the language, I first needed to define what valid tokens of the language look like. The easiest way to do that is by looking at the grammar of a language, so I determined the grammar for the example file above. I’m not going to explain how exactly I did that (in short, I drew a lot of inspiration from the C grammar), but here is the result.
rule-list = rule
| rule-list rule
rule = identifier ':' logical-OR-pkgex ';'
logical-OR-pkgex = logical-AND-pkgex
| logical-OR-pkgex '||' logical-AND-pkgex
logical-AND-pkgex = primary-pkgex
| logical-AND-pkgex '||' primary-pkgex
primary-pkgex = literal operator identifier
| '(' logical-OR-pkgex ')'
operator = '>' | '>=' | '<' | '<=' | '==' | '!=' | '=~'
identifier = string | literal
A string is a double-quoted sequence of characters just like in C, and a literal is
something like a variable name in C, but with . allowed as part of the name. Version
numbers like 1.2.3 are also literals.
The lexer should identify all terminals in the language, which are all symbols that never appear on the left-hand side of any grammar rule (grammar rules are also called productions). In the grammar above, the terminals are strings, literals, and everything in single-quotes.
Writing the lexer
Shell does not have classes or structs, and passing data from a function to its caller in variables is very awkward and should be avoided if at all possible. Really, the only practicable way to pass data back to the caller is via standard output. It is nevertheless possible to write a very elegant lexer: with a set of recursive functions that read an input character by character and write the recognized tokens to standard output.
The tokenize() function is the entry point and forwards the input to one of the more
specific tokenizer functions. The specific tokenizer functions expect two arguments,
the portion of the input that was already processed and not written to stdout yet, and
the portion of the input that has not been processed yet. The tokenizer function then
looks at the next character of the input and decides whether to print a token to
standard output and what tokenizer function to call next. Formally speaking, the
tokenizer is a state machine and each tokenizer function represents one state.
tokenize() {
local input="$1"
case "${input:0:1}" in
'<'|'>'|'!')
tokenize_cmp_op "${input:0:1}" "${input:1}"
;;
'=')
tokenize_eq_op "${input:0:1}" "${input:1}"
;;
# ...
esac
return "$?"
}
tokenize_cmp_op() {
local read="$1"
local input="$2"
if [[ "${input:0:1}" == "=" ]]; then
echo "RELOP:$read${input:0:1}"
tokenize "${input:1}"
else
echo "RELOP:$read"
tokenize "$input"
fi
return "$?"
}
tokenize_eq_op() {
local read="$1"
local input="$2"
case "${input:0:1}" in
'='|'~')
echo "RELOP:$read${input:0:1}"
tokenize "${input:1}"
;;
*)
echo "RELOP:$read"
tokenize "$input"
;;
esac
return "$?"
}The drawback of this approach is that the depth of the recursion grows with the size of the input, but – speed aside – this worked fine with all inputs that I threw at the script. I’m not including the entire tokenizer in this post, but you can find it on Github.
From tokens to trees
To see how we can use the grammar from earlier to turn a stream of tokens into a parse tree, it’s helpful to have a look at a simple rule and the tokens that the lexer returns when reading it. This will be a little theoretical, but I will try not to make it too boring. Let’s assume we have a file with only the simplest of the three rules from above.
BaseOS : name =~ "^miraclelinux-";
There are six tokens in this input, namely the following.
LITERAL:BaseOS
COLON::
LITERAL:name
RELOP:=~
STRING:^miraclelinux-
SEMICOLON:;
The first production in the grammar of our language is for rule-list, so this is
where the parser will start. It will then attempt to derive the right side of the
production from the tokens in the token stream. For every production that it
successfully parses, it will generate a node and add it to the parse tree. In this
example, the parser would start with a rule-list, then derive a list, which in
turn contains an identifier, a colon token, a logical-OR-pkgex, and a semicolon
token. From the logical-OR-regex production it would derive a logical-AND-pkgex,
and from this one it reaches the production for primary-pkgex, which can be
produced with the tokens name, =~, and ^miraclelinux- that are next in the
token stream. When the parser returns to rule-list, there are no more tokens in
the stream, and since the production it parsed does not need more tokens, it is done.
The parse tree that the parser generates in this way looks like the following.
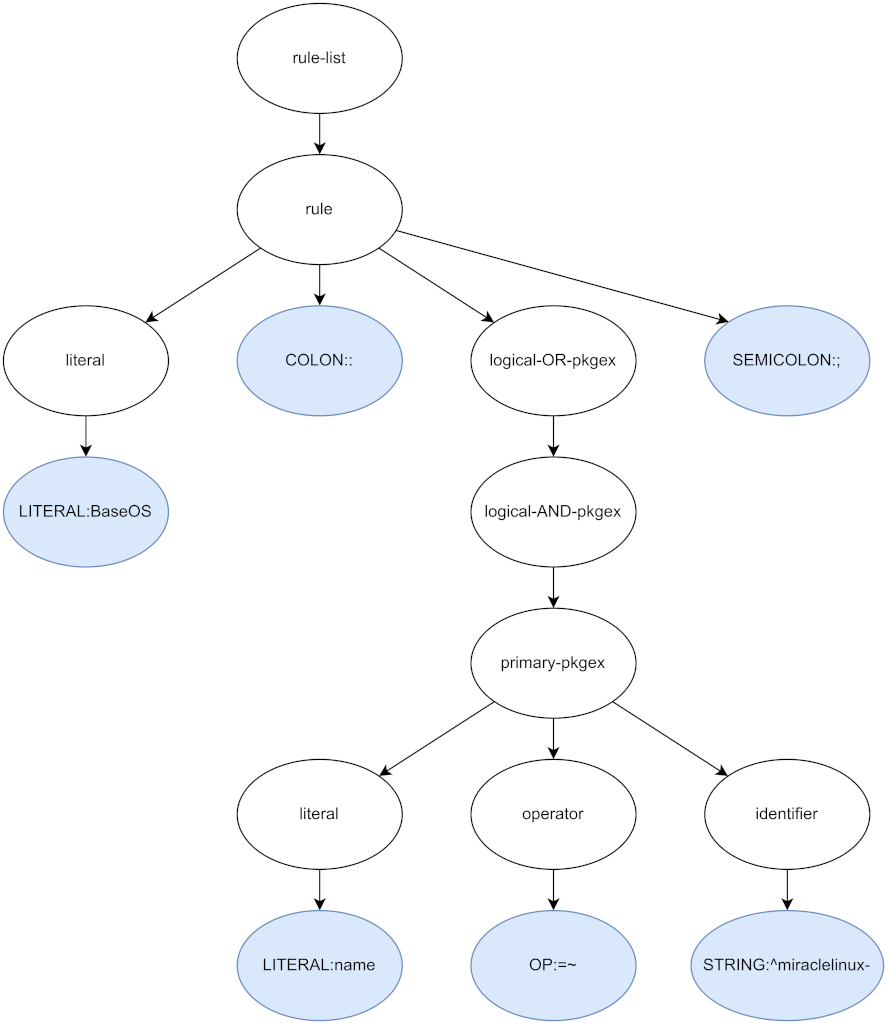
Because the parser recursively descends the productions of the grammar, it is called a recursive descent parser. It uses a grammar to anticipate the structure of the input, making it a syntax-directed parser. Parsers like this are typically implemented with a set of functions, each of which parses one symbol of the grammar.
Let’s have a look at one of the simple cases, parse_string(). This function expects
the next token in the token stream to be a string (the token stream is passed
in the arguments). If this expectation is met, the function emits a node for the token
to stdout, otherwise it returns an error.
parse_string() {
local token="$1"
if [[ "${token%%:*}" != "STRING" ]]; then
return 1
fi
node_new 1 "STRING" "s:${token#*:}"
return "$?"
}The call to node_new() is what generates the actual node. It creates a JSON object
with three properties num_tokens, type, and data, and writes it to standard
output.
The first parser function that is slightly more complicated is parse_primary_pkgex(),
which implements the following productions.
primary-pkgex = literal operator identifier
| '(' logical-OR-pkgex ')'
Because primary package expressions can take two different shapes, the function has to decide which one to parse. The second shape always starts with an open parenthesis, so a look at the next token is enough to decide how to continue. The next token, as well as the concept of looking at it to make parser decisions is called lookahead.
When a decision has been made, all that parse_primary_pkgex() has to do is call the
parser functions for the symbols that the productions expect, and generate a node for
the result – or return an error.
parse_primary_pkgex() {
local tokens=("$@")
local -i tokens_used
local data
if [[ "${tokens[0]}" == "LPAREN:(" ]]; then
# primary-pkgex = '(' logical-OR-pkgex ')'
local lparen
local pkgex
local rparen
lparen="${tokens[0]}"
tokens_used=1
if ! pkgex=$(parse_logical_or_pkgex "${tokens[@]:$tokens_used}"); then
log_error "Expected logical-OR-pkgex near \"${tokens[*]:$tokens_used:1}\""
return 1
fi
(( tokens_used += $(node_get_num_tokens "$pkgex") ))
rparen="${tokens[$tokens_used]}"
if [[ "$rparen" != "RPAREN:)" ]]; then
log_error "Expected ')', found \"$rparen\""
return 1
fi
data=$(json_object "lparen" "$lparen" \
"child" "$pkgex" \
"rparen" "$rparen")
(( tokens_used++ ))
else
# primary-pkgex = property operator identifier
local property
local operator
local identifier
if ! property=$(parse_literal "${tokens[@]}"); then
log_error "Expected literal, found \"${tokens[0]}\""
return 1
fi
tokens_used=1
if ! operator=$(parse_operator "${tokens[$tokens_used]}"); then
log_error "Expected operator, found \"${tokens[$tokens_used]}\""
return 1
fi
(( tokens_used++ ))
if ! identifier=$(parse_identifier "${tokens[$tokens_used]}"); then
log_error "Expected identifier, found \"${tokens[$tokens_used]}\""
return 1
fi
(( tokens_used++ ))
data=$(json_object "property" "$property" \
"operator" "$operator" \
"identifier" "$identifier")
fi
node_new "$tokens_used" "primary-pkgex" "$data"
}Primary package expressions are not recursive (at least not in the way
logical-OR-pkgex grammars are), so while the function is somewhat lengthy, it
doesn’t have any complicated logic.
Dealing with left-recursion
This brings us to parse_logical_or_pkgex(), which parses package expressions with
a logical or conjunction. Let’s have another look at the grammar.
logical-OR-pkgex = logical-AND-pkgex
| logical-OR-pkgex '||' logical-AND-pkgex
The production to derive a logical-AND-pkgex is as simple as could be, but it’s the
second production that will give us a headache if we try to implement it with pure
recursion. Because the production derives itself as the left-most non-terminal, it is
said to be left-recursive. Left-recursive grammars cannot be parsed with a purely
recursive algorithm.
This is one of those cases, where the iterative appoach is much simpler anyway: we
start by parsing a logical-AND-pkgex and, as long as it is followed by a logical or
operator, we loop to parse more. Because the grammar is left-recursive, we have to
construct the parse tree in reverse order, creating a new node during each iteration
and nesting the node from the previous iteration into the new one. Even though this is
arguably more complicated than the parser for primary-pkgex grammars, it is much
shorter, and I would even dare to say it is much more readable. The other left-recursive
grammars can be parsed with exactly the same approach, so I won’t bother discussing the
rest of the code here. You can find the code on Github.
parse_logical_or_pkgex() {
local tokens=("$@")
local -i used_tokens
local logical_or_pkgex
used_tokens=0
logical_and_pkgex=""
while true; do
local logical_and_pkgex
local operator
local data
if ! logical_and_pkgex=$(parse_logical_and_pkgex "${tokens[@]:$used_tokens}"); then
log_error "Expected logical-AND-pkgex near \"${tokens[$used_tokens]}\""
return 1
fi
(( used_tokens += $(node_get_num_tokens "$logical_and_pkgex") ))
operator="${tokens[$used_tokens]}"
data=$(json_object "right_child" "$logical_and_pkgex" \
"operator" "$operator" \
"left_child" "$logical_or_pkgex")
logical_or_pkgex=$(node_new "$used_tokens" "logical_or_pkgex" "$data")
if [[ "$operator" != "OR:||" ]]; then
break
fi
(( ++used_tokens ))
done
echo "$logical_or_pkgex"
return 0
}By the way, if the production were right-recursive, we would not have to construct the
parse tree in reverse order. As a result, the expression would be evaluated from right
to left. As a rule of thumb, expressions like a || b || c that are evaluated from
left to right have left-recursive productions, and expressions like a = b = c that
are evaluated right-to-left have right-recursive productions.
Trial run
Now that lexer and parser are done, they can be pieced together with a short script like the following. It expects the path of an input file in the first argument, reads the contents, tokenizes them, parses the token stream, and writes the resulting parse tree to standard output. I omitted a lot of error handling for the sake of brevity. If you’re coding along, don’t forget to check return values and validate user inputs. :-)
#!/bin/bash
main() {
local input_file="$1"
local input
local tokens
if ! input=$(<"$input_file"); then
echo "Could not read $input_file" 1>&2
return 1
fi
readarray -t tokens < <(tokenize "$input")
parse "${tokens[@]}"
}
{
main "$@"
exit "$?"
}Now we can pass the example file from the top to our parser and we’ll get a minimized
JSON object that we’ll pipe through jq to pretty-print it.
$ ./parser.sh example.pkgex | jq '.'
{
"num_tokens": 42,
"type": "rule_list",
"data": {
"rule": {
"num_tokens": 14,
"type": "rule",
"data": {
"repository": {
"num_tokens": 1,
"type": "LITERAL",
"data": "AppStream"
},
"colon": "COLON::",
"pkgex": {
"num_tokens": 11,
"type": "logical_or_pkgex",
"data": {
"right_child": {
"num_tokens": 11,
"type": "logical_and_pkgex",
[...]
Pretty neat, right? That’s how you write a recursive descent parser in Bash. And I bet it isn’t nearly as bad or unreadable as you expected. :-)
Nevertheless, it’s hard to overstate how slow it is, and that is why I ended up rewriting it in Python. The script that evaluates parse trees is even slower, but it might still make an interesting read. That’s for another time, though.
Code on Github
You can find the code in the following repository. Note that it depends on toolbox for the modularization.